Stations With Lowest Probability of Busting a Call: CQ WW CW 2005 to 2016

Prior posts in this series:

• Initial analysis
• Further analysis
• CQ WW SSB 2005 to 2016

In this post I list the stations with the lowest probabilities of busting a call in CQ WW CW from 2005 to 2016, using the procedure developed in the second post above. This is the same methodology as was used in the third post.

2005 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	LZ9R	0.0008	1210	0
2	HI3/SP9XCN	0.0008	2403	1
3	K1TO	0.0010	992	0
4	OK1FDR	0.0011	888	0
5	W5MX	0.0012	826	0
6	DK1MAX	0.0013	717	0
7	OK1JOC	0.0014	701	1
8	DL6KVA	0.0014	698	0
9	OM8ON	0.0014	693	0
10	DF1DX	0.0015	656	0

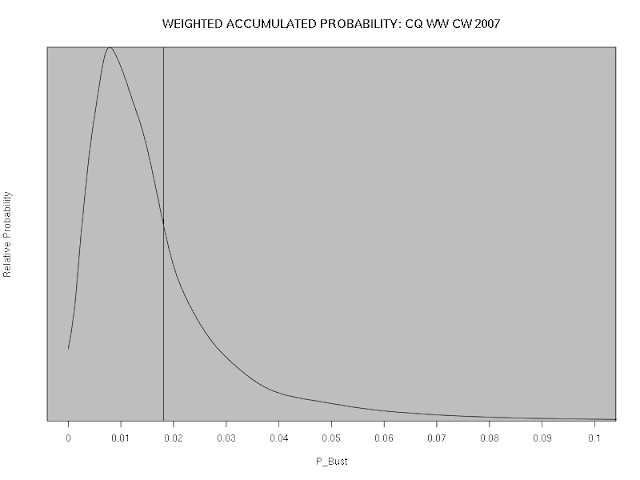
As with SSB, we plot the aggregated probability function for $p_{bust}$, weighted by the number of verified QSOs, $Q_v$, for all stations:

As before, the location of the vertical line represents the weighted mean of the probability curve.

2006 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	DL5KUT	0.0007	1288	0
2	LY2MM	0.0008	1223	0
3	I2WIJ	0.0009	1091	0
4	OH8X	0.0009	2235	1
5	DL8DYL	0.0010	982	0
6	9A3GI	0.0010	953	0
7	HB9ARF	0.0012	802	0
8	WE9V	0.0013	747	0
9	K1HT	0.0014	710	0
10	KR2Q	0.0014	693	0

2007 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	SM6CNN	0.0007	1267	0
2	DL8DYL	0.0008	1151	0
3	SP2LNW	0.0010	967	0
4	KQ3F	0.0012	828	0
5	W2LE	0.0012	784	0
6	TM6A	0.0012	1614	1
7	N9CK	0.0013	765	0
8	K8CC	0.0013	763	0
9	UA1CUR	0.0013	760	0
10	W1MU	0.0013	744	0

2008 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	S56A	0.0007	1368	0
2	K6NA	0.0010	997	0
3	HA8FW	0.0011	900	0
4	DL1RG	0.0012	785	0
5	N9CK	0.0012	772	0
6	LY3BG	0.0014	684	0
7	K5ZD	0.0014	2827	3
8	PA0JNH	0.0015	640	0
9	JS3CTQ	0.0015	631	0
10	OK1JOC	0.0016	1287	1

2009 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	N4BP	0.0008	1229	0
2	LZ2SX	0.0008	1135	0
3	K1ZZ	0.0009	1009	0
4	W3OA	0.0010	988	0
5	OM0WR	0.0010	923	0
6	OK2BUT	0.0012	791	0
7	EY8MM	0.0013	735	0
8	JP1QDH	0.0013	729	0
9	SM0Q	0.0014	709	0
10	KR2Q	0.0014	702	0

2010 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	YT2AAA	0.0007	1418	0
2	N2GC	0.0008	1200	0
3	SP9NSV	0.0008	1188	0
4	OK7T	0.0010	969	0
5	RZ3VO	0.0011	892	0
6	W6OAT	0.0012	806	0
7	VA7RN	0.0012	771	0
8	OH8FKU	0.0013	741	0
9	OH6MW	0.0013	2267	2
10	G4HZV	0.0014	683	0

2011 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	LZ2SX	0.0007	1296	0
2	OR2F	0.0007	1293	0
3	W1ZT	0.0007	1266	0
4	W3OA	0.0008	1212	0
5	RN1ON	0.0008	1134	0
6	LZ9R	0.0008	2407	1
7	RG5A	0.0009	1080	0
8	UN9GD	0.0009	1079	0
9	US2IZ	0.0009	1050	0
10	DL1DVE	0.0010	951	0

2012 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	HB9ARF	0.0006	1601	0
2	JI1RXQ	0.0006	1514	0
3	DJ1YFK	0.0007	1266	0
4	DL4FN	0.0008	1166	0
5	SM6FKF	0.0009	1069	0
6	ES1WST	0.0009	1040	0
7	AD1C	0.0010	984	0
8	SM6CNN	0.0010	976	0
9	LY3CY	0.0011	895	0
10	SM5CIL	0.0011	887	0

2013 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	K1TO	0.0006	1569	0
2	VX7SZ	0.0006	1491	0
3	LY2NY	0.0006	1439	0
4	W2LE	0.0007	1369	0
5	IK8UND	0.0007	1297	0
6	UA3MIF	0.0009	1037	0
7	LY3CY	0.0010	985	0
8	N0BK	0.0010	955	0
9	OM0WR	0.0010	949	0
10	AA7V	0.0011	900	0

2014 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	S54X	0.0005	2005	0
2	KM3T	0.0005	1829	0
3	5H3EE	0.0006	1637	0
4	S56A	0.0006	1622	0
5	OH6MW	0.0007	3024	1
6	YT2AAA	0.0007	1376	0
7	AD1C	0.0007	1337	0
8	UW1WU	0.0007	1317	0
9	K2MK	0.0007	1302	0
10	M6W	0.0009	2267	1

2015 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	K6LL	0.0005	1922	0
2	LZ9R	0.0007	2833	1
3	K7UA	0.0007	1254	0
4	JI1RXQ	0.0008	1219	0
5	DH0GHU	0.0008	1216	0
6	RG5A	0.0008	1127	0
7	OM0WR	0.0008	1119	0
8	RX1A	0.0009	1099	0
9	RD9CX	0.0009	1093	0
10	RW5CW	0.0009	1071	0

2016 CQ WW CW -- weighted mean values of $p_{bust}$
Position	Call	weighted mean	$Q_v$	$B$
1	LY5W	0.0005	1850	0
2	KE3X	0.0006	1633	0
3	DM2M	0.0006	1563	0
4	K0KX	0.0007	1389	0
5	K1ZZ	0.0008	2555	1
6	RX7K	0.0009	1031	0
7	EW8W	0.0009	1017	0
8	K2PO	0.0010	977	0
9	OL4W	0.0010	975	0
10	LY3CY	0.0010	955	0

NB: As mentioned in the SSB analysis, it is, of course, much easier to copy a callsign correctly if one calls stations rather than running them. Indeed, a reasonably careful station that restricts itself to calling others should never make a mistake in copying a callsign. In the above analysis, there is no attempt to distinguish which station is calling which. Therefore we will refine this analysis in a later post, restricting it to running stations.

As with SSB, one thing stands out from the above plots: the distribution function for $p_{bust}$ across all entrants is remarkably robust. Here is a plot of the weighted mean of $p_{bust}$ as a function of time (the CW data are red; the SSB data are superimposed in black):

Just as for SSB, the long-term trend is for an improvement in accuracy, but the last few years seem to have stabilised around a mean weighted probability of a bust of about 1.6%. It is clear that the bust rate for CW is persistently better by a small amount than the rate for SSB (which is perhaps a surprising result).

If you wish to perform your own analyses, a file of the CW weighted means of the $p_{bust}$ probability function for each individual station (not just the top-ten stations listed above) is available for the period 2005 to 2016. (You can, of course, create your own dataset(s) from the full augmented data files.)